Posts Tagged notation
Gamelan & Sonic Youth
In many ancient traditions and contemporary settings, music is not written out for the performance. It’s worked out among the musicians, maybe by a lead composer type all at once, or by the group over a period of time. The piece or song is memorized and maybe at some point has a life outside that group of musicians, so it becomes like an oral tradition of storytelling.
So, let’s say you wanna write that down. Seems reasonable that you’d try to do this with the tools you have, which is staff notation invented for western orchestral music. But unless the musicians in question were also trained in this method and set out to follow the rules as such, you are going to end up with a crude approximation. Two examples I’ve been really interested in over the years is traditional Balinese Gamelan and the 80s-90s work of punk/art rock group Sonic Youth.
Worth noting that Gamelan music has a native written form (a few in fact), and that the harmonic ideas of SY have roots in the music of avant garde composer Glenn Branca, who has his own presumably meticulous system. But in practice, both of these types are just winging it. In addition to not adhering to a preexisting written standard, they also both are using either bespoke or customized instruments and tunings. (Really hate the use of “bespoke” to mean “custom” but it fits here.) A Gamelan orchestra—all the gongs and metallophones—are made as a piece, tuned to itself. Each player isn’t bringing the reyong or gangsa they are leasing from Guitar Center, these things only exist together as one thing and can’t be individually adjusted. If one were lost or broken, you can’t even swap one out from another group. Likewise, when SY’s van was stolen in 1999, the sound of the band was heavily impacted. They were touring with 24 heavily customized guitars; almost a different set for each song. All of the older songs from that point had to be reworked and relearned.
Here’s the most comprehensive list of SY tunings, which, despite appearing to be a fan site in design and guesswork is in fact their official site. The band themselves apparently did not keep exact notes and any 3rd party’s detective could be just as good. I have even seen versions that note differences in the unison tunings (i.e. “second D slightly flatter”) and this is where a decimal system of tuning would really be helpful.
It’s these slight differences that create a sound totally different than what can be achieved through normal western intonation. The shimmering textures most…notable…here are created very deliberately (tho not always exactly or uniformly) by the dissonances that are reduced or edited out completely of regular music.
The very complex numbers that you can wind up with when referring to a note by it’s frequency in Hz can be replaced with a simple “𝑥.𝑥𝑥” by using the 0-11 formula and then the deviation .01-.99 in cents, ultimately leading one to a very snappy conclusion.
A New Kind of Numerical Notation
Important development in the comments section of the last post of the Numerical Notation category. In fact it was the not only the most recent post, but the final post before changing the name of the category, which is now: A0̸
I’ve tried to make it look nice and unambiguous, but it can be commonly known as “A0 Notation”, pronounced “A-Zero” or if you prefer, “A-Oh”.
As suspected, there is already an almost identical system. It is called Integer Notation. Very easy to search for if you know what it is called, and also supposedly easy to find if you’re stumbling around music theory wikis so that’s slightly embarrassing. It is also used in the John Woo film Hard Boiled which is even more annoying to me because I have to admit I hadn’t seen it before a few days ago:
I first figured this was something unrelated made up for the movie, a trivial point. But no, it’s really standard Integer Notation. [Ed: Not quite, there’s no zero. It’s using the numbers 1-7 for the diatonic scale, regardless of key.]* The above is the melody line for Lionel Ritchie’s Hello, written in C:
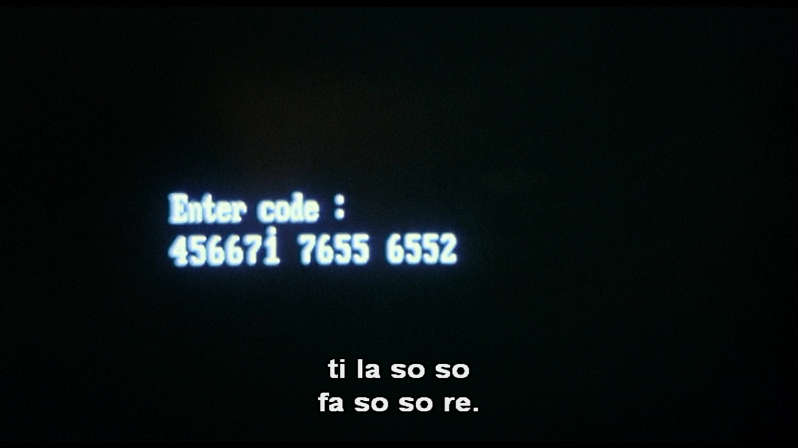
F=1 here. And they’re also using the “movable do” Solfege system. So I don’t have to point out that this form of numerical notation is just a form of that which is easier to input into a DOS computer from the 80s, but I will. Done.
So whadda I got? Mine would be a “fixed do” system where A=0, but it’s 12-tone so forget about the “do” thing. Remember the the charts I made for the saxes in different keys? Probably not but forget those too, gotta make new ones. That system just makes it easier to sight-read staff notation—once you learn the fingerings for one sax, you can play any (theoretically) just pick up any sax and start sight-reading that part, and you just have to not think about how the notes coming out of the horn are totally different. I don’t think my system can replace lettered notation or staff notation entirely but I think it could in a lot of situations, especially learning where you should be internalizing the names of the concert pitch notes regardless of your instrument of choice.
So I’ll just be making some new charts then. %
*Altho it could be considered a ~type~ of "Integer Notation", what's used is the movie actually might be unrelated and just made up for the movie and therefore, in fact, trivial. But it's still a fun example of alternate notation.
Numerical Notation: A Minor Threat
Hoo boy. Year of the Sheep, right? Some people only seem to notice when it’s a “cool” animal like a dragon or a snake. We have a name for these people: DILETTANTES. There’s nothing cool about sheep, except this Minor Threat cover, so get used to seeing that I guess. But wait, it’s the Year of the Ram, isn’t it? Rams are cool. What with the head-butting and…that’s it. It’s enough. Give rams a chance. Or goats, who cares.
But I’m not here to review Minor Threat. Or talk about astrology. I’ve listened to enough Minor Threat for a lifetime (since I bought the Complete Discography on CD, in 2006) and it’s unlikely to make it back in rotation, unlike the Chinese Zodiac which repeats every twelve years…of course.
Forget all this happened.
Shit, that’s still the title isn’t it. Look, I’m gonna explain.
I’ve made a system of numerical notation. I call it Numerical Notation. The notes of the chromatic scale are given the number 0-11, starting with A.
In this system, if you care about the Modes (which you should, if you care about why there is a lettered system) the Aeolian mode, or A Minor, is the base scale, not C Major(the Ionian). It’s debatable that A Minor was historically, originally the more important. I think it sounds better. That’s not important. The important thing is to make this a non-vague point. Because I have noticed some other examples using notes for numbers starting with C as 0. I even said in earlier posts that you might as well do this if it makes more sense, but it doesn’t, in the big picture, and I’m gonna make the case that this is not some kind of arbitrary nerd bullshit dicking-around.
Here we are then with example one:
The sharp/flat system has been primarily designed for use in the major/minor system; when speaking modally, it’s a lotta look, to quote a famous fashion designer. All the flats and sharps tend to obscure the simplicity […] We need a different system of talking about melody. If C is assigned the number 0, C# the number 1, all the way up to B = 11, we can study the system numerically, and also universally, as any tonic can be assumed. Zero can just as easily be G#, or E. Also, since the tonic can never change by our definition, it’s not necessary to include it. Here’s an example to show what I’m talking about.
C Mixolydian is C D E F G A Bb C. If we assume that C = 0, and continue from there, then C Mixolydian can also be described as 0 2 4 5 7 9 10 12.
This post is excellent and you should read the whole thing. I should read the whole thing. The point is that here is someone making essentially the same point as me, naming the notes 0-11 (12=0), but starting with C. (Note that is doesn’t predate my initial posts.) Not saying he stole it, but I also said it was an “open source” idea, which is a pretty dumb way to talk because it is not a computer program. But I guess that can be interpreted as “feel free to steal this idea”. I was drinking a lot at the time. It’s not like you can patent this kind of thing anyway.
But let’s run with the open source concept and say he explained the idea better. I’m gonna bring it back around and explain why it’s easier for everyone if A=0.
But first(second), example two:
This is from a video that goes on to explain a new type of keyboard layout for an experimental instrument called a Terpestra. Now this is the kind of thing you can patent and even sell. Good luck to him. Again, not saying he stole the idea. Even if he did, can you really expect drop-in citations in a video like this? It’s not relevant who came up with each idea in this kind of presentation. It’s also kind of an obvious idea once it’s out there. Not as obvious as starting with 1 tho.
But it’s about to get even more obvious. Check this out:
Ａ ａ# Ｂ Ｃ ｃ# Ｄ ｄ# Ｅ Ｆ ｆ# Ｇ ｇ#
０ １ ２ ３ ４ ５ ６ ７ ８ ９ １０ １１
Ｃ ｃ# Ｄ ｄ# Ｅ Ｆ ｆ# Ｇ ｇ# Ａ ａ# Ｂ
Which one of these makes more sense? You might still pick C if you are already trained in music, but how would you explain that to a student? The letters and numbers should be going in the same direction. It’s intuitive.
If you never start, you can never branch out into other things, like the higher concepts these other guys are talking about and the simplest way is the best way to start.
So while you are thinking about all this, here’s a video of GWAR covering the Pet Shop Boys:
%
Numerical Notation and the 3rds Tuning for 7-String Guitar
I’m unfortunately averaging a post a month at the moment as I’ve had to prioritize finding more gainful employment (29 hrs/wk @ min. wage would do it), also Japanese class, which I could see myself teaching. But what about music? Never even considered teaching music. And yet I’m kinda doing it. For free. Oops. Well, you’ve gotta start somewhere.
But there’s not much of a market for a completely ground-level reinvention of musical notation. It just seems crazy. However, inventing this system has allowed me to teach myself how to explain regular music to myself, which really is crazy…..IS. IT. SO. “CRAZY”? Not really it’s all pretty boring, I’m just trying to be dramatic to keep your interest. You can give up now. It’s not interesting. It’s pretty dumb. But let me ask you a question: how do you feel about sleep? I’m ambivalent about the whole thing. I mean after work, looking for more work, and the occasional video game, sleep can really put a dent in the ol’ blog schedule.
Where was I? Oh right, proving the inferiority of an unjustly ingrained, non-intuitive note naming system. Here ya go:
I’ve been thinking about getting a 7-string for a while and using the 3rds tuning on it. The extra string not on;y offsets the loss of range with the tuning, it creates a something perfectly even and symmetrical. Which is just nice, it’s got nothing to do with anything. It’s just that with traditional 4ths tuning, to get the top string and bottom string 2 octaves apart, you throw in that 3rd. And that does make some chords easier to play, but it’s always bugged me. It’s tricky to name the notes in any particular chord right off the top of your head. (Which is real easy on the piano.) Playing the chords and scales is almost all about memorization, which is why so few guitarists use alternate tunings, even when the instrument is so easy to tune and retune to almost anything. The proof is right above. I did not do this on purpose, but I just wrote out this chart real quick, and I did it to show other guitarists so I’m using regular letter notes, and “steps”. Several guitarists (and one professional cellist!) saw the post and liked it with no comment. Later I noticed the number of steps I’m saying to move up or down is wrong in multiple places. This is because it’s not a standard number of steps that neither I or most guitarists have memorized.
Most common example is taking the E string a step down to a Dropped D tuning. But taking E up to F is only a half step. Because there is no E#. (There is, E#=F.) Likewise for B#. This should of course also be memorized to the point of not having to think about at all. But that’s not the same thing as an intuitive system. It’s the illusion of one. Create an unusual case that never comes up and even pros (even proams on the internet, who live to point out mistakes like this) can be fooled at first glance. (Which is the only glance most things on the internet get anymore.)
Instead, numerically:
Standard 7-string tuning (low to high):
2 7 0 5 2 7
3rds tuning starting on A:
0 4 8 0 4 8 0
3rds tuning starting on C#/Db:
4 8 0 4 8 0 4
You can immediately see the number of half steps you need to move then without barely even thinking about it and get some goddamn sleep already. %
Numerical Notation for Saxophones Revisited
Been thinking about getting back into the sax. I could never be a great player, especially after taking so many years off, but it’s fun to play the horn, any horn, even if you are just making noise. I’d was thinking about getting a C Melody because I’ve just been working with guitar, bass and piano for several years and now I’ve got an ear for the real note values (not the Bb or Eb values) that I don’t want to mess up. I turns out the C melody sounds an octave lower than concert pitch. What I really want then is a C soprano, the only sax that plays the exact concert notes.
Except I don’t want to do that. Look, it doesn’t matter what I want. I’m kinda tired right now. But I haven’t posted in month and I need to keep going here. It was a nice break. But no one else really cares about this project at the moment, so it’s all me. And this has been bugging me. So I made some index cards like before, but less half-assed. (Have I mentioned repeatedly a major strength of numerical notation is the ease with which you can write it on ordinary index cards? It’s just something I noticed is handy.)
So I just went through the main saxes (including the C ones nobody really uses) and located middle C & A440. It’s as much for myself as anyone who is interested. (Which is maybe nobody. But maybe you. It’s only you… Did you know A440 is the highest regular note on a bari sax, if it has the extra key? I didn’t.) Here you go, and I hope it is helpful:
%
繕った [records tumblr]
Visitors
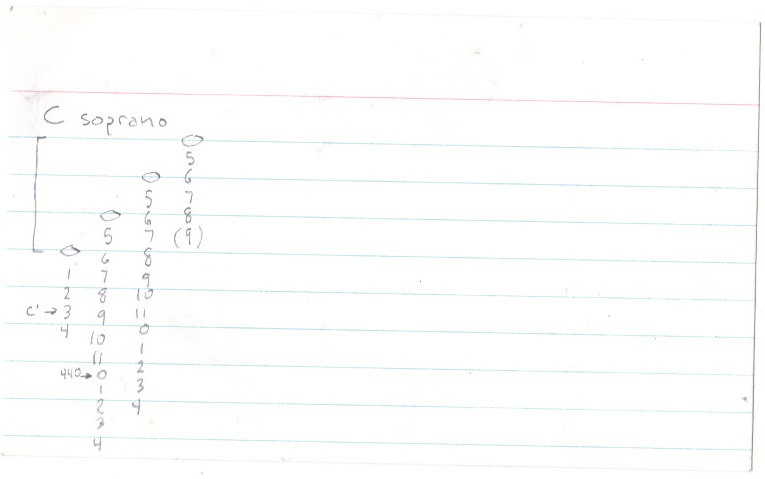
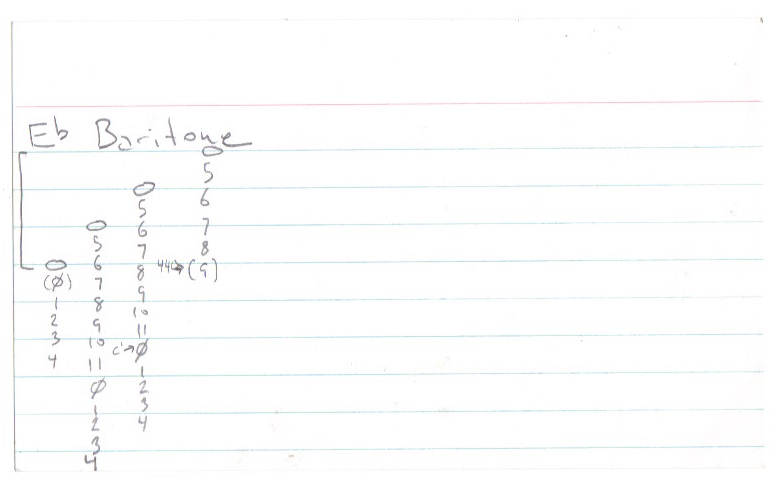
Recent Comments