Archive for category ＤＰ⓪
Continuing Numerical Notion
I get that this whole idea makes it seems like turning music into math and that is going to seem uncool to some people. I am not trying to make math seem cool. Advanced math is interesting to me because it’s completely beyond my comprehension. I know that it makes sense, but I don’t know how. I’ve never been a math nerd. Trying to explain music theory to someone who understands Calculus and Physics like it’s something that don’t immediately understand fully already makes me seem like the moron I am.
This is not advanced math, it’s very simple. Think about why Math sucks, C- minus Algebra I students who taught themselves guitar or whatever. It’s the bullshit like memorizing multiplication tables and equations, right? It’s the exact opposite of fun. Advanced Music Theory is kinda the same thing. You’ve probably noticed this if you tried to pick up a book on it but didn’t want to admit it. It’s not the subject matter, it’s the thought process. The Circle of Fifths is just like multiplications tables. They just tell you it makes sense without explaining it and you have to drill it and memorize it. Most people just muddle through. If you do learn it, you just know it without really understanding why it works. That’s my experience. Musicians (even some teachers) either don’t learn theory or don’t really understand it.
I think there’s a way to break it down. Just like you can break multiplication down into addition. It takes a little longer at first, because if you just memorize the answers you can just spit them out. But with practice, it’s gonna be just as fast and eventually you’ll know it the same, but you’ll also know the reason for the answer.
When you use numbers for the notes, the interval is apparent through simple subtraction. Here’s a chart for the differences:
1=minor 2nd (half step)
2=major 2nd (whole step)
3=minor 3rd (step & a half)
4=major 3rd
5=perfect 4th
6=tritone (aug. 4th/dim. 5th)
7=perfect 5th
8=minor 6th
9=major 6th
10=minor 7th
11=major 7th
And of course a difference of 12 is back to the same number an octave higher or lower. I’m working on a modified staff system to make this practically useful as written music for an instrument. But you’ve got to understand how this works as a concept first.
At this point you might be thinking this is not very useful for music that spans more than one octave, which is most music you’d want to listen to. Or hell, even any scale that doesn’t start at 0 has to cross over 0 and why are we doing this again? You’ve got to keep in mind that with lettered notation you’re doing the same thing with arbitrary values. The note after G is G# and the note after that is A. Then A#, then B, then C. Quickly then, what is the interval between A and C? You can either memorize that this is minor 3rd, or you can subtract 0 from 3. Easy. But what about G to C? It’s better to think of it like a clock:
image courtesy internet clock store, whatever
It helps to be on military time. You’re going to have to trust me on this. %
Understanding Why Lettered Notation is Illogical
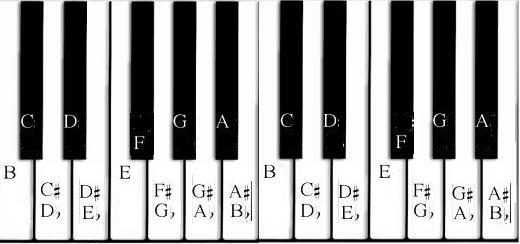
Music is not Science. There’s some interesting sciencey things about music, but music itself doesn’t have to perfect or logical. Classical notation using letters is a great example. It hasn’t changed for hundreds of years altho the values and assignments are largely arbitrary. Here’s the notes on a keyboard:
Most pianos and keyboards will be tuned to A440 in equal temperament. Some have an issue with this but my beef is the assignment of the black and white keys, or really the concept of flats and sharps as they are assigned to the letters A-G.
The argument against redesigning this system from scratch may be that music is more about intuition than logic and that the existing system has prevailed precisely because of this and anyway, it’s all pretty logical it you study it long enough. But this is the problem. It only seems right because you accept these arbitrary assignments as a kind of Truth that is unquestioned. Staring from this, a logical construct is formed around it that supports itself and eventually, seems intuitive. But really, the process involves rote memorization which is wholly unintuitive. For example, the notes A and B are a whole step apart, but B and C are a half step. Why? There is a historical reason, but also, the notes themselves must be considered as nonsense. The white keys on the piano may seem “brighter” sounding or more “natural” in some way but this is only through repetition, ear training, and relative placement of notes. An older standard of note values places the A above middle C at around 415 Hz, a full half-step below A440. If a keyboard is tuned to the values of the notes when those notes were invented, the keyboard looks like this:
(it actually will look the same if you don’t paint the note values on there)
Unless you have perfect pitch (trained to 440), you might not even notice a piano has been tuned this way. It might sound off at first, but you’d get used to it. Time has proven this. The system of equal temperament is another example, but regarding the intervals. We are accustomed to hearing notes and intervals slightly wrong from what they were first intended to the point were the “right” values now sound wrong. Eliminating the arbitrary system of letter values with sharps and flats would make learning notes and intervals easier for new students.
%
Intro to Numerical Notation
You don’t need an introduction to the idea of numerical notation if you are not classically trained on a guitar or piano. There’s tablature and chord numbering systems that work well enough that there’s often no need for a player to learn to read notes on a staff, especially if they stick to standard tunings.
I first learned music in elementary school on the clarinet, which is in Bb. In high school I switched to Alto Sax, which is in Eb. Then I started learning guitar on my own and quit the school band. I messed around with the tunings a lot. I tried taking and advanced music theory class but failed it. I aced the basic test, but I could not name the notes on the piano by ear for my life. Some people in the class had only just started on the piano or guitar and seemed to have no problem. It’s probably a crushing defeat I would not keep going back to mentally if I had since succeeding at something else in life, but here we are.
In the dark and disturbing future we currently live in, “the kids” can get into music without ever learning any real physical instrument. A few years ago, I got into an argument about flats and sharps in different keys. The argument goes that that you don’t really need both flats and sharps; the names of different keys and scales contain the same notes with different names. (For example, you could always use sharps.) If the music only exists in the computer, the names of the notes don’t matter. I figured this could be taken a step farther to eliminate both flats and sharps:
Ｏ｜１｜２｜３｜４｜５｜６｜７｜８｜９｜１０｜１１｜Ｏ
This is what I came up with. That is an A chromatic. Each number is a half-step and now it’s perfectly clear what intervals you are dealing with for any scale you make. There’s a slight problem of ‘１０’ & ‘１１’ taking up two spaces instead of one I haven’t worked out yet, but I’ve also given the notes one syllable names that can be as read quickly as “do-re-mi”, etc. Not quite as nice sounding, but less relative:
- Ｏ – A —— (“oh”)
- １ – A#/Bb — (“wun”)
- ２ – B —— (“tu”)
- ３ – C —— (“tri”)
- ４ – C#/Db — (“for”)
- ５ – D —— (“fiv”)
- ６ – D#/Eb — (“sik”)
- ７ – E —— (“sev”)
- ８ – F —— (“eht”)
- ９ – F#/Gb — (“nin”)
- １０ – G —— (“ten”)
- １１ – G#/Ab — (“lev”)
It’s also less relative in that it’s strictly nailed to A440 and equal temperament. This is simply because it’s most widely used. But because it’s numbers, any variation can be expressed in decimals. A44x for example would be Ｏ.x, and A415—A3xx would be １１.x (you’d have to figure out the exact math). This is not practical at all for sight reading in most cases of course, but it gives the note a definite value that can be applied to any octave or transposition. It also accurately names microtones, with quartertones being named ‘x.５’, which could get confusing if you use a lot of them, like if you’ve got a piano tuned to quartertones, but you probably don’t.
These are all things I can explain more later.
%
-
You are currently browsing the archives for the ＤＰ⓪ category.
繕った [records tumblr]
Visitors
Recent Comments