Archive for category DP⓪
Numerical Notation and the 3rds Tuning for 7-String Guitar
I’m unfortunately averaging a post a month at the moment as I’ve had to prioritize finding more gainful employment (29 hrs/wk @ min. wage would do it), also Japanese class, which I could see myself teaching. But what about music? Never even considered teaching music. And yet I’m kinda doing it. For free. Oops. Well, you’ve gotta start somewhere.
But there’s not much of a market for a completely ground-level reinvention of musical notation. It just seems crazy. However, inventing this system has allowed me to teach myself how to explain regular music to myself, which really is crazy…..IS. IT. SO. “CRAZY”? Not really it’s all pretty boring, I’m just trying to be dramatic to keep your interest. You can give up now. It’s not interesting. It’s pretty dumb. But let me ask you a question: how do you feel about sleep? I’m ambivalent about the whole thing. I mean after work, looking for more work, and the occasional video game, sleep can really put a dent in the ol’ blog schedule.
Where was I? Oh right, proving the inferiority of an unjustly ingrained, non-intuitive note naming system. Here ya go:
I’ve been thinking about getting a 7-string for a while and using the 3rds tuning on it. The extra string not on;y offsets the loss of range with the tuning, it creates a something perfectly even and symmetrical. Which is just nice, it’s got nothing to do with anything. It’s just that with traditional 4ths tuning, to get the top string and bottom string 2 octaves apart, you throw in that 3rd. And that does make some chords easier to play, but it’s always bugged me. It’s tricky to name the notes in any particular chord right off the top of your head. (Which is real easy on the piano.) Playing the chords and scales is almost all about memorization, which is why so few guitarists use alternate tunings, even when the instrument is so easy to tune and retune to almost anything. The proof is right above. I did not do this on purpose, but I just wrote out this chart real quick, and I did it to show other guitarists so I’m using regular letter notes, and “steps”. Several guitarists (and one professional cellist!) saw the post and liked it with no comment. Later I noticed the number of steps I’m saying to move up or down is wrong in multiple places. This is because it’s not a standard number of steps that neither I or most guitarists have memorized.
Most common example is taking the E string a step down to a Dropped D tuning. But taking E up to F is only a half step. Because there is no E#. (There is, E#=F.) Likewise for B#. This should of course also be memorized to the point of not having to think about at all. But that’s not the same thing as an intuitive system. It’s the illusion of one. Create an unusual case that never comes up and even pros (even proams on the internet, who live to point out mistakes like this) can be fooled at first glance. (Which is the only glance most things on the internet get anymore.)
Instead, numerically:
Standard 7-string tuning (low to high):
2 7 0 5 2 7
3rds tuning starting on A:
0 4 8 0 4 8 0
3rds tuning starting on C#/Db:
4 8 0 4 8 0 4
You can immediately see the number of half steps you need to move then without barely even thinking about it and get some goddamn sleep already. %
Numerical Notation for Saxophones Revisited
Been thinking about getting back into the sax. I could never be a great player, especially after taking so many years off, but it’s fun to play the horn, any horn, even if you are just making noise. I’d was thinking about getting a C Melody because I’ve just been working with guitar, bass and piano for several years and now I’ve got an ear for the real note values (not the Bb or Eb values) that I don’t want to mess up. I turns out the C melody sounds an octave lower than concert pitch. What I really want then is a C soprano, the only sax that plays the exact concert notes.
Except I don’t want to do that. Look, it doesn’t matter what I want. I’m kinda tired right now. But I haven’t posted in month and I need to keep going here. It was a nice break. But no one else really cares about this project at the moment, so it’s all me. And this has been bugging me. So I made some index cards like before, but less half-assed. (Have I mentioned repeatedly a major strength of numerical notation is the ease with which you can write it on ordinary index cards? It’s just something I noticed is handy.)
So I just went through the main saxes (including the C ones nobody really uses) and located middle C & A440. It’s as much for myself as anyone who is interested. (Which is maybe nobody. But maybe you. It’s only you… Did you know A440 is the highest regular note on a bari sax, if it has the extra key? I didn’t.) Here you go, and I hope it is helpful:
%
Staff System for Numerical Notation
I made some quick sketches for my idea for a new type of staff system to get it out there. Each octave gets a line and the numerical value is written directly below. The standard graphical system for time value of the notes (whole/half/quarter/etc.) can still apply. Y’know, if yr into that sort of thing. (Shown is whole notes.) This is not written as something you’d play—altho technically you could mash down 12 keys at a time—it’s just an idea what it would look like:
Note that this is for a grand piano with 88 keys starting on low A. Most keyboards start on C and have less octaves. If you’re writing everything like it’s going to be performed by an orchestra, conventional methods are just fine and you certainly don’t need help from a moron like me. However, I find that the goal of writing music like that is little much for a student and not what they want to do anyway. So the task of writing music seems impossible and they never even really try it. This system is instrument specific; whatever keyboard you’ve got gets it’s own kind of staff. So it’s not some abstract system of every possible note you are dealing with, which you then apply to the instrument and see it if can hit it, but a very clear layout of all the notes available to you on the instrument in front of you.
Let’s take a closer look at how this works on another instrument: the saxophone. Various saxophones come in different ranges and keys, but the fingerings for the named notes are always the same. (Except some have a low A key or a high F#.) But the octave doesn’t start on the A for the the sax, it starts on D. It’s purely a mechanical feature of the instrument:

(A440 is going to be in a different spot for alto/tenor/etc.—it’s where things get complicated. Don’t worry about it.)
Now, if you know anything about the saxophone, you can see I’ve made a terrible mistake and left out an entire octave. This is not really a problem right now, because like the earlier posts, if I just put this thing out all at once looking great and making sense, some asshole is just going to put it on a t-shirt and no one will care where it came from. And of course, hardly anyone would use this system for piano or saxophone, it’s mostly useful for string instruments that can alter their tuning and range. (And maybe even for singers.) If you can figure out how to do this already, good for you. But I’ll keep working on better ways to present the idea. %
Numerical Notation vs. Scientific Pitch Notation
I’ve been hoping to come up with something snappier than “Numerical Notation”, but it seems to be sticking so maybe it’s snappy enough. I think it’s unique enough to avoid confusion with other notation systems that may use numbers but not numbers exclusively. For example, Scientific Pitch Notation.
Scientific Pitch Notation is not to be confused with regular old Scientific Notation and it won’t be, so let’s stop worrying that. And don’t think I’ve got some beef with science over 4ths and 5ths. I’m not saying it’s magic, it’s just something very interesting that does not have an easy, intuitive explanation. If it did, every music teacher would just tell you the first day of class and every book on music would have in the first few pages, instead of just trudging you through all the stuff to memorize and hoping you don’t notice until it’s far too late for you to do anything else with your life but teach the exact same system and the whole cycle perpetuates.
Is it so bad? Maybe. Can you make through the second paragraph of this entry without your eyes glazing over? Because that’s a less subjective question. Giving numbers to each octave on the piano is a great idea, but there’s just this silliness with starting the octave on C I can’t get over. A is the first letter and the first key. Why not make more of those last high notes the freak notes? (What I’m trying to do here is make this system sound even less “scientific” than my own fudging of the term. Is it working? Works for me.)
Ah, and there’s the staff. SPN changes nothing about that. Trad bass and treble clefs. Can’t improve on that. Could improve on the tone of these posts, probably, but is that important, and can I end this sentence without making it another annoyingly rhetorical question—a habit that I can’t believe I’ve picked up as it annoys even me—I think I can. I’ve done it, yes. No, not that. Designed a new staff system. Well, I haven’t really done it, I’ve just thought about a lot. (Not a metaphor.) It’ll have to wait for another post. %
Numerical Notation and the 4ths vs. 5ths Paradox
There’s a smart sounding title, wonder if I’ve got anything to back it up.

Here’s the clock again from last post. The idea of naming the notes with numbers within an octave is dead simple. Scientifically speaking, two notes with a 2:1 ratio might as well be the same note.
YET,
It is not so. 0+5=the perfect 4th; 5+0(the octave above)=a perfect 5th. A simple counter-intuitive fact I have never heard explained or even alluded to in any music class or lesson. There are the Circle(s) of Fifths/Fourths presented to be memorized, but never explained. (This post is no exception.) But the simpler image of the clock with numbers can help. The 5th is thought of as the center of the diatonic scale, but chromatically it is the tritone. From any numbered note, we can see its tritone directly opposite on the clockface. And the fourths and fifths are not merely about counting semitones but knowing which direction they are coming from and going. 5 places clockwise is the 4th and 7 is the 5th and vice versa. Then when you get into extended chords and intervals you can see the value of the 24hr clock. Memorizing these values is much simpler than letters with arbitrary accidentals. So there. %

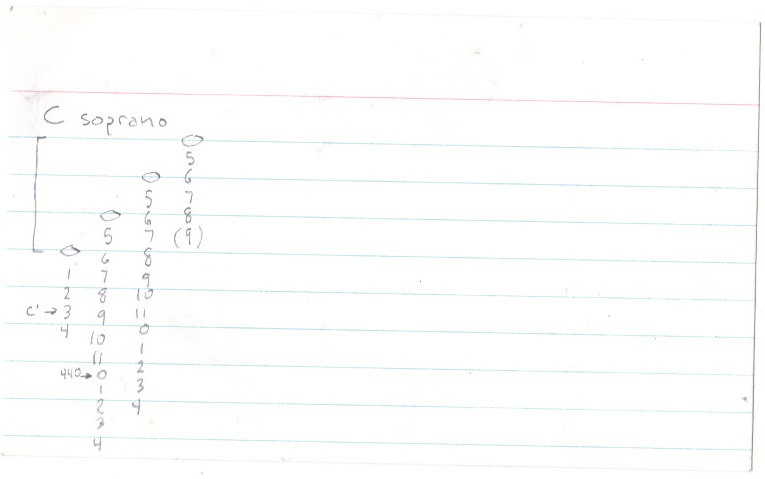




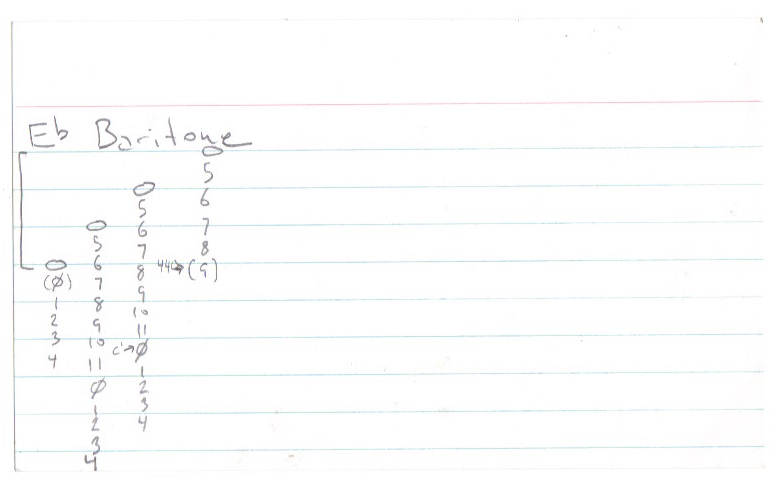







Recent Comments