Archive for category DP⓪
Fixed Interval Notation: Why…are you? Doing this! To me!?
Look, you came here, alright. This whole thing could be meaningless. I mean everything. But let’s not worry about that. What is just this thing about? Let’s think about Jimi Hendrix again. Most people will say he tuned his guitar to E♭, sometimes D; that is, tuning to the entire guitar down a half or whole step. (It’s complicated by analog recording and playback, the standard of those days. If the speed of either changes, the pitch changes.) If you aren’t using a tuner, this sometimes becomes the default accidentally by tuning to the top string (standard E) which naturally becomes flatter over time. If the notes really matter in themselves, this would change the name of every scale and chord that you play. It doesn’t. That’s because you aren’t tuning to E♭, you are tuning to A=415 or thereabout.
And this is The Problem that led me to this Whole Thing. Learning music as a kid on a horn or strings, you learn that the instrument tends to go flat, and when the orchestra plays in a group it tends to be flatter than the piano. This is known as classical pitch and it’s about A=430. It’s a good idea to have the standard be a little sharp, right? So you tune to the piano and it lands in the ballpark. (If you are playing along with a piano, you’d want it to stay there as close as possible. Most beginner orchestras don’t play along with a piano.) But I’ve gone back and researched it, and you can read the wikis I hope, it’s not just a small adjustment to the standard historically. It really was 415 and one point, which is fully A♭ today. At another point in Germany it became 466, which is A♯ (or B♭). Take a look at the keyboard:
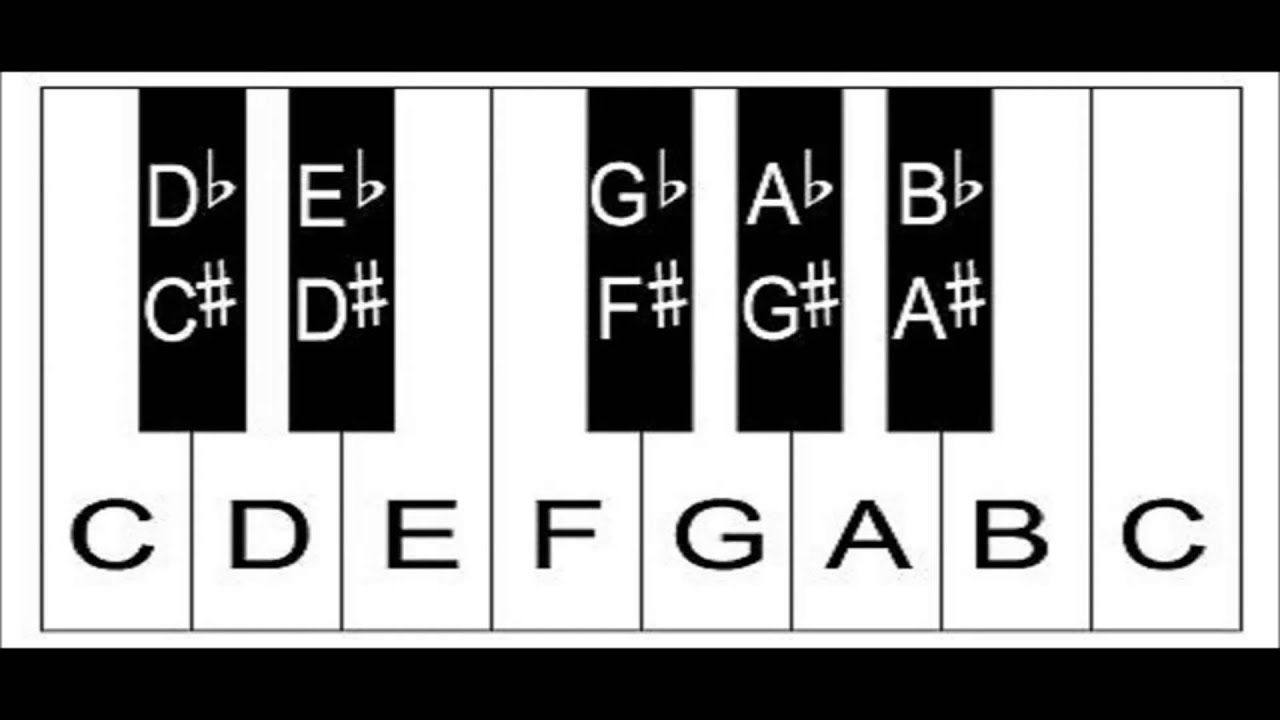
If you shift the tuning a half-step in either direction you get chaos with the the names of the notes. But there’s nothing special about the frequencies themselves that make the white keys the Natural Notes, and the black keys Accidentals (in the Key of C Major, A Minor or any of the traditional church modes). Think about the Modes. They are the first scales in Western music, right? That’s why it’s those keys. But to really hear how they sounded, you have to shift them down a half step. Seems…crazy. But isn’t that WHAT THEY WANT YOU TO THINK? No. It’s not. If “they” is music teachers, they definitely don’t want you to think about this because it’s really distracting and YOU’VE GOT TO FOCUS.
Fixed Interval Notation: Limits of Use
Hm, sounds legal. Not really, but it’s occurring to me now I’m making a system that’s more for analyzing than composing. Having some latitude with changing what frequency the note “A” is, for example, is pretty useful is some cases. Jimi Hendrix, for example, tended to tune down his guitar a little, probably just by ear. In FIN the note might be called 11, or 11.5, or 11.75. The more complex a number it is, the harder it is to read off the page. But if you just want to know what the exact note someone else is playing, it is useful information. I’ve tried making a simple equation to translate the frequencies (in Hz.) to simple decimal numbers, but you run into a problem pretty quick. Let’s ease into this with this very simple, randomly selected video:
Now it gets a little more complicated:
So you see there’s some more work to do. Think about it.
Against Reaction
Occurred to me that most people are not aware how pervasive equal temperament is. Just want to make it clear that this is not part of some kind of reactionary movement is favor of the most conventional music possible. It’s simply acknowledging that most music you encounter in the modern world can be played on a standard piano or digital keyboard, and that it’s tuned to A=440 Hz. Not only is this true of almost all pop music and western classical music, it’s true of almost every anarchist punk band, hip-hop producer, bedroom recordist and free jazz musicians up to the point of noise. Most atonal music is still using equally tempered notes; it only forgoes regular scales, and most experimental music that intentionally deviates can be measured in it’s deviation from equal temperament*. It’s not an ideology, it’s a fact of life in the modern music world.
Up next: more on this.
*(which was my original purpose, I think)
Extended Intervals

Remember this? Don’t worry about it.
Y’know, people kinda take the 7 note diatonic scale for granted. This is why it might be confusing when you name the notes chromatically, as we (um, just me so far really) do in this system. When you think of the octave (literally “the eighth”) as “12” it reveals the fact that 4 notes that are left out of the regular scale.
Of course there’s also the pentatonic scale that leaves out two more. That kind of scale is really the most common is all the history of all music of the world, also unequally tempered. I’ve thought about this a lot, and I haven’t reached the conclusion that the equal tempered, 12-note system is the absolute best possible. But it’s not bad. I have to ask people that have dedicated their lives to fighting it: Can you not make good music with it? Do you really hate MOST music you hear?
I’m really against the idea of just taking it for granted that it’s the ONLY way to make music (i.e. “There’s only 12 notes!”) But the idea that it’s complete garbage and that the only good music either only existed in the past (before records, we don’t know what it really sounded like) or can only exist in some ideal future state when we finally figure this shit out (again, unhearable) is dumb. Not to create a strawman, there are many classical and experimental musicians that accomplish what they trying to prove, and make fantastic sounding music. But many seem to think they don’t know what music is supposed to sound like, and that it may even be impossible to know. I suggest listening to the music that exists.
That said, there is more than the very simple 2-7 intervals and there’s a different way to think about them. Also, I can make a list now:
- minor 9th = 13
- major 9th = 14
- minor 10th = 15
- major 10th = 16
- perfect 11th = 17
- Aug. 11/Dim. 12 = 18
- perfect 12th = 19
- minor 13th = 20
- major 13th = 21
- minor 14th = 22
- major 14th = 23
- perfect 15th/double octave = 24
Later!
Thinking about Intervals
Integer Notation doesn’t reinvent music theory, it just gives a different way to describe the notes. I’ve been thinking lately about how it might clash with other systems using numbers, like the Nashville Number System for chords or the tab system for guitar. Both of these are too useful to discard for a whole new system and maybe it’s too complicated to be using more than one at a time.
But I think as long as it’s clear what system it is at what time, it’s a small mental adjustment to use the same numbers for different things. For example, the names of the intervals. They do not need to change, in fact we can make them clearer by translating the difference between two numbered notes into the traditional names:
unison = 0
minor 2nd = 1 (2-1)
major 2nd = 2
minor 3rd = 3
major 3rd = 4 (3+1)
perfect 4th = 5 (4+1)
tritone = 6 (3 whole tones)
perfect 5th = 7 (5+2)
minor 6th = 8 (6+2)
major 6th = 9 (6+3)
minor 7th = 10 (7+3)
major 7th = 11 (7+4)
octave = 0 (12 = 8+4)
Man do I hate how WordPress works anymore. Can’t make a simple list? Well that’s my one idea for now.






Recent Comments